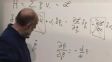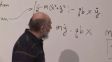Classical Mechanics

Fall, 2007

Our exploration of the theoretical underpinnings of modern physics begins with classical mechanics, the mathematical physics worked out by Isaac Newton (1642--1727) and later by Joseph Lagrange (1736--1813) and William Rowan Hamilton (1805--1865). We will start with a discussion of the allowable laws of physics and then delve into Newtonian mechanics. We then study three formulations of classical mechanics respectively by Lagrange, Hamiltonian and Poisson. Throughout the lectures we will focus on the relation between symmetries and conservation laws. (Image credit: The International Astronomical Union/Martin Kornmesser)

iTunes Playlist
YouTube Playlist

Lectures in this Course

  1. 1
    Lecture 1 | Modern Physics: Classical Mechanics (Stanford)

    State diagrams and the nature of physical laws

    This first lecture is a general discussion of the nature of the laws of physics and in particular classical mechanics. The notions of configuration, reversibility, determinism, and conservation law are introduced for simple systems with a finite... [more]
  2. 2
    Lecture 2 | Modern Physics: Classical Mechanics (Stanford)

    Newton's laws, principle of least action

    Consider Newton's law relating force and acceleration. Define kinetic energy and potential energy. Derive conservation of energy for a system of particles. Define the Lagrangian and derive the Principle of Least Action starting from Newton's Law. ... [more]
  3. 3
    Lecture 3 | Modern Physics: Classical Mechanics (Stanford)

    Euler-Lagrange equations, symmetry and conservation laws

    Define the Euler-Lagrange equations as a result of the Principle of Least Action. Define the canonical momentum. Differential conservation laws result from a continuous symmetry.
  4. 4
    Lecture 4 | Modern Physics: Classical Mechanics (Stanford)

    Symmetry and conservation Laws

    This lecture focuses on he relation between continuous symmetries of the Lagrangian and conserved quantities. Generalized coordinates and canonical conjugate momentum are introduced.
  5. 5
    Lecture 5 | Modern Physics: Classical Mechanics (Stanford)

    Lagrangians and Hamiltonians

    Example simple pendulum:  derive the Euler-Lagrange equations, the kinetic energy, potential energy, Lagrangian and angular momentum. Calculate the Hamiltonian. Review the trajectory of the simple pendulum in phase space. Derive conservation of area... [more]
  6. 6
    Lecture 6 | Modern Physics: Classical Mechanics (Stanford)

    Hamilton's equations

    The Hamiltonian function determines the evolution of a system Closed cycles in phase space represents a conservation law Hamilton's equations are first order equations of motion. Newton's equations are second order equations of motion. Canonical... [more]
  7. 7
    Lecture 7 | Modern Physics: Classical Mechanics (Stanford)

    Liouville’s theorem

    Prove Liouville’s theorem from Hamilton’s equations. Liouville’s theorem can be thought of as information conservation. The laws of mechanics are equivalent to the rules governing state transition. Ignored degrees of freedom, such as friction, can... [more]
  8. 8
    Lecture 8 | Modern Physics: Classical Mechanics (Stanford)

    Motion in an electromagnetic field

    Recapitulate symmetries and conservation laws. According to Liouville's theorem, a system evolving according to Hamilton's equations conserves the volume of phase space. Information is conserved. The Principle of Least Action underlies Lagrangian... [more]
  9. 9
    Lecture 9 | Modern Physics: Classical Mechanics (Stanford)

    Poisson brackets formulation

    Poisson brackets formulation describes flow in phase space. Define the axiomatic structure of Poisson brackets. Canonical rransformation of Poisson brackets preserves the Poisson bracket axioms. Define the generator of an infinitesimal canonical... [more]